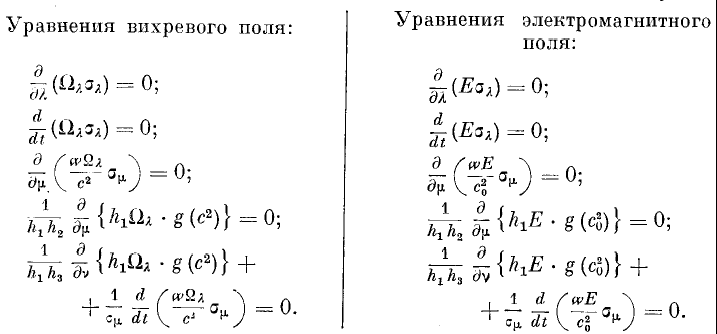
Слияние аэродинамики и электродинамики
В декабре 1936 года на особом совещании при Академии Наук были представлены математические исследования Кастерина в виде доклада под названием “Обобщение основных уравнений аэродинамики и электродинамики”. Вызывает большой интерес его несколько частных решений. Изложим вкратце суть работы Кастерина несколько измененными выдержками из доклада.
В качестве точки отсчета исследований он сделал допущение, что уравнения Эйлера и Максвелла не точны абсолютно, а являются первыми приближениями. Критериями приближения в аэродинамике можно использовать отношение квадрата скорости движения газа к квадрату скорости звука в нем, а электродинамике – отношение квадрата скорости движения электрического поля к квадрату скорости света. При изыскании вторых приближений Кастерин имел в виду, что возможны случаи скоростей движения равных или даже больших, чем скорость звука и соответственно скорость света. При выводах уравнений Эйлера и Максвелла постулировалась непрерывность строения газа и электрического поля. Кастерин же решил учитывать экспериментальные факты прерывности. Полученные Кастериным уравнения для движения газа чрезвычайно мало отличаются по внешнему виду, но имеют другие частные решения. Например, в случае уравнений Эйлера для невихревого уравнения газа вокруг цилиндрического вихря получается парадоксальный вывод: судя по формулам, вихревое движение в такой форме невозможно осуществить. Однако в опыте легко получить вихревой столб между двумя параллельными плоскостями, на которые вихрь опирается своими концами. И решения Кастерина совпадают с опытом - кинетическая энергия обращающегося вокруг вихря газа конечна и убывает с увеличением расстояния от центра. На уравнениях Эйлера базируется теория вихрей Гельмгольтца. По этой теории вихрь есть довольно мимолетное явление, вихревые движения легко возникают и так же легко исчезают. Уравнения Кастерина дают возможность объяснить и существование необычайно устойчивых вихрей в виде смерчей. Выведена формула зависимости напряжения вихря от его угловой скорости. Оказалось, что напряжение вихря имеет максимум при некотором значении угловой скорости, то есть вблизи этого максимума вихрь обладает наибольшей устойчивостью. Величина этого максимума определяется тремя физическими параметрами: адиабатным коэффициентом, скоростью звука и числом Авогадро. Для воздуха получается, что линейная скорость на периферии вихря равна скорости звука, поперечник вихря равен 10 метров, а угловая скорость порядка 10 об/сек. Все свидетели, наблюдавшие смерчи в наиболее разрушительной их стадии, оценивают их поперечные размеры именно в 10 м.
Из уравнений второго приближения для аэродинамики следует неожиданный результат: масса вихря за все время его движения остается неизменной. Важное следствие: если за счет работы внешних сил вихрь поделится, то масса дочерних вихрей восстановится до родительской массы за счет притекающего извне незавихренного до того газа. И наоборот, объединившиеся два вихря в единый вихрь сбрасывают излишки массы в окружающую среду. По теории Гельмгольтца объяснить такое невозможно. Кроме того, в единственном случае, при адиабатной константе k=2, имеет место сохранение напряжения вихря, то есть вихрь вполне устойчив. Для известных газов k<2 и вихревое движение неустойчиво. Только для какого-то сверхгаза (k=2) вихревое движение устойчиво.
Оказалось, что между уравнениями второго приближения для электродинамики и уравнениями второго приближения для аэродинамики для сверхгаза (при k=2) существует полный параллелизм. Для удобства сравнения мы можем опустить в уравнении электромагнитного поля постоянные величины и тогда получаем:
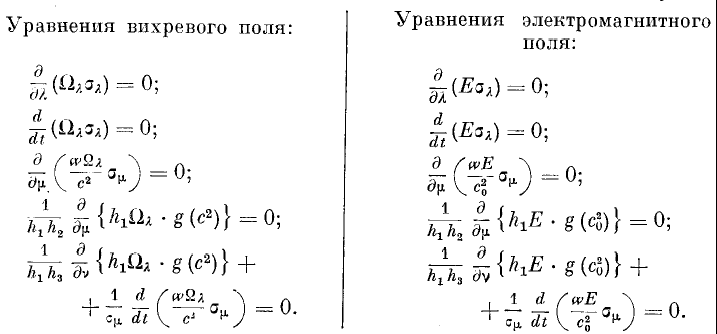
Если допустить, что для сверхгаза скорость звуковая равна скорости света, то получается, что элементарный электрический заряд пропорционален массе, распределенной на сечении элементарного вихря. При такой материализации само понятие “заряд” теряет свой прежний смысл, и его можно употреблять только как меру элементарного “потока электрической индукции”. В уравнениях электродинамики скорость света величина постоянная, а в уравнениях аэродинамики скорость звука есть функция времени и координат. Только этим отличаются уравнения. Кастерин предложил и скорость света считать функцией, тогда в качестве обобщенных уравнений электромагнитного поля можно принять полностью все уравнения вихревого поля. Результирующие уравнения отличаются от уравнений Максвелла не только тем, что они не линейны, но и тем, что скорость света внутри поля переменна. Вследствие нелинейности уравнений мы обязательно придем к решению по крайней мере квадратного уравнения для компонентов поля, откуда следует, что обобщенные уравнения могут дать нам вид поля только в ограниченной части пространства, так как для остального пространства компоненты будут иметь мнимые значения. Но из общего выражения для кинетического потенциала Н для движения системы вихрей оказывается, что фактор g можно представить как
![]()
Здесь п – любое целое число (но не слишком большое), положительное или отрицательное, и нуль в том числе. Тогда имеет место еще целая система дифференциальных уравнений подобного вида. В результате такая система уравнений с различными значениями g определяет электромагнитное поле во всем пространстве, занятом системой вихрей или электромагнитным полем.
Кастерин нашел два простейших частных решения для поля, создаваемого электроном. В первом решении поле имеет вид тонкого слоя (с угловой толщиной f0) на поверхности усеченного конуса с углом f=90град-f0. Направление поля приблизительно определяется логарифмической спиралью на поверхности поля. Во втором решении получается поле в виде слоя на воронкообразной поверхности, начинающейся у начала координат, и поле направлено по образующим этой поверхности. Эти два решения действуют совместно, так как имеют место в разных частях пространства. Поле симметрично относительно плоскости, проходящей через начало координат и перпендикулярной к оси вращения, то есть электрон состоит из двух симметричных половин.

Рисунок 1. Изображения вихревого газового объекта – геометрического аналога структуры электрона по математическим выкладкам Кастерина
Кастерин привел к единому виду уравнения электродинамики и уравнения аэродинамики. Это означает, что можно найти геометрическую аналогию структуры электрона среди вихревых газовых объектов. Если он не ошибся при поиске двух частных решений, то простейшей геометрической интерпретацией этих решений является комбинированный газовый вихревой объект из двух винтовых тороидов, слипшихся торцами в плоскости зеркальной симметрии. На рисунке 1 изображена поверхность такого объекта. Слева на рисунке – вид с торца, правее - вид со стороны ребер нормальный и в разрезе, еще правее - разрез одного тороида. Плоскость, проходящая через место слипания (разрез C-C), является плоскостью зеркальной симметрии. Тороидальное вращение обоих тороидов с внешней стороны ребра направлено к плоскости симметрии, а с внутренней стороны – от плоскости симметрии вдоль оси симметрии. Кольцевое вращение обоих тороидов сонаправлено, поэтому комбинация имеет ненулевой момент вращения. Разрез A-A проходит через ось симметрии, вокруг которой тороиды совершают кольцевое вращение. При повороте комбинации на 180 градусов в плоскости, проходящей через ось симметрии, момент вращения меняет знак.
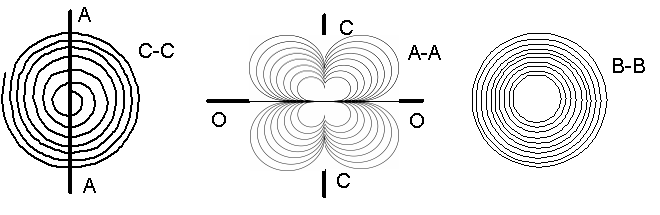
Рисунок 2. Вращение слоев окружающей газовой среды вокруг геометрического аналога электрона по математическим выкладкам Кастерина
Внутри объема, ограниченного поверхностью максимальной плотности, скорость вращения должна резко падать по экспоненциальному закону. На разрезе A-A показано направления потоков газа за пределами изображенной поверхности с максимальной плотностью. То есть, за ее пределами газ тоже вращается, только скорость вращения падает с увеличением расстояния от центра комбинации. Если попытаться изобразить поверхность с некой скоростью вращения, меньшей максимальной скорости на заданную величину, то получим ту же самую картинку слипшихся тороидов, только более крупных размеров. В плоскости зеркальной симметрии (разрез С-С) окружающий газ по логарифмической спирали втягивается во внутрь вихревой комбинации. И выбрасывается из торцов комбинации вдоль оси симметрии OO (из центра на разрезе B-B). Первое частное решение Кастерина похоже на разрез С-С с физически бесконечно малой угловой толщиной. Второе частное решение Кастерина – два конуса джетов с очень малым телесным углом вдоль оси симметрии, исходящие в разные стороны из центров двух торцов вихревой комбинации.
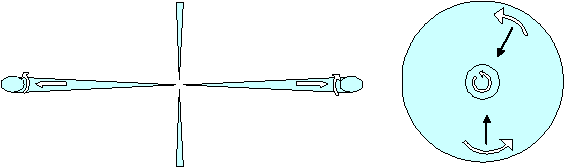
Рисунок 3. Поверхности двух частных решений Кастерина для электрона
Поверхность максимальной плотности данного газового объекта локализована в пространстве, но вращение окружающей газовой среды должно распространяться до бесконечности, с вовлечением во вращение все новых и новых слоев газа, при стремлении к нулю скорости вращения слоя. Поведение газа вдоль оси симметрии и в плоскости симметрии совпадает с выводами Кастерина. Только вращение окружающих слоев не локализовано, а непрерывно распространяется в бесконечность. Если объект смещается в пространстве, то вращение начинает заново распространяться от поверхности максимальной плотности газа. Но ранее вовлеченная во вращение газовая среда продолжает некоторое время вращательное движение уже без воздействия объекта и может взаимодействовать с новыми возмущениями от смещенного в пространстве объекта, формируя волновые явления. Кастерин пытался объяснить волновые свойства электрона тем, что вращающееся электрическое поле электрона образует в незавихренной области волны сгущения и разряжения. Если он прав, то такой эффект способен создавать либо пульсирующий (осциллирующий) объект, либо объект движущийся по спиральной траектории. Для данного газового объекта и такое поведение при движении вполне естественно.
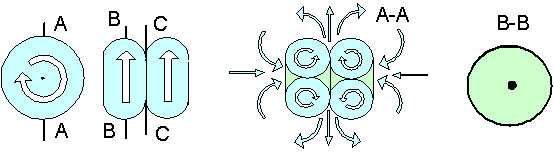
Рисунок 4. Геометрический аналог структуры позитрона по математическим выкладкам Кастерина
В зависимости от соотношения направлений кольцевого и тороидального вращения, винтовые вихревые тороиды можно подразделять на левовинтовые и правовинтовые. Кроме того, у каждого тороида можно выделить передний торец и задний торец. Винтовой тороид имеет способность самостоятельно без приложения внешних сил двигаться передним торцом вдоль оси симметрии. Из переднего торца газ извергается, а в задний торец газ втягивается. В комбинации из двух тороидов левовинтовой и правовинтовой вихревые тороиды соединены задними торцами, в результате чего стремление к движению тороидов взаимно компенсируется, способность к самостоятельному движению теряется. Если левовинтовой и правовинтовой вихревые тороиды слипнутся передними торцами, то получится другой вихревой объект, у которого газовые потоки имеют противоположное направление. Этот объект можно рассматривать в качестве геометрического аналога структуры позитрона.
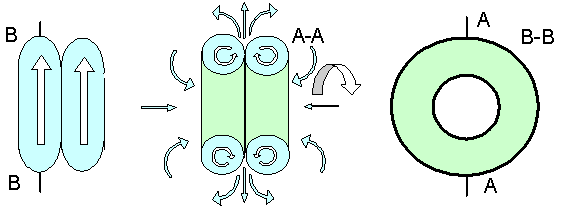
Рисунок 5. Геометрический аналог структуры протона по математическим выкладкам Кастерина
Для случая протона по формулам Кастерина вид поля более подобен вихревому полю в случае смерча. Под его два частных решения неплохо подходит другой комбинированный газовый вихревой объект - два винтовых кольца, слипшиеся торцами в плоскости зеркальной симметрии.
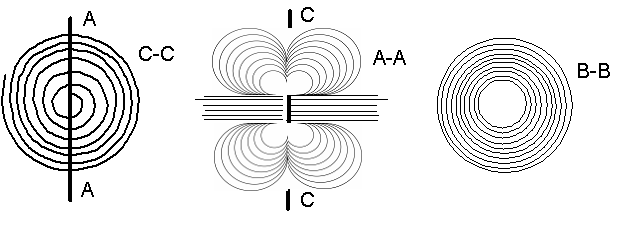
Рисунок 6. Вращение слоев окружающей газовой среды вокруг геометрического аналога протона по математическим выкладкам Кастерина
Вихревые тороиды, составляющие вихревую модель протона, скорее всего должны быть похожими на бублики, то есть внутренние отверстия тороидов соизмеримы с размерами тороидов. В этом случае формируемые моделью протона во внешней окружающей среде вихревые потоки будут отличаться от потоков, формируемых моделью позитрона, только вдоль оси симметрии. В модели протона вдоль оси симметрии формируются два цилиндрических вихря, втягиваемых в отверстия тороидов. А в плоскости зеркальной симметрии газ извергается из газового объекта, вращаясь по логарифмической спирали.
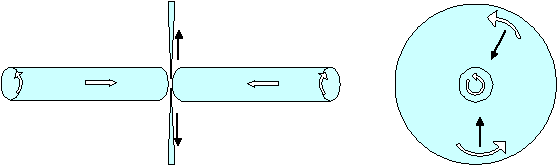
Рисунок 7. Поверхности двух частных решений для протона
Если два винтовых кольца, составляющие вихревую модель протона, слипнутся противоположными торцами, то получится вихревая модель антипротона.
Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru , июль 2006