Пики удельной энергии ядер

Удельная энергия связи ядра быстро растет у легких ядер, имеет максимальное значение в районе железа - никеля и медленно уменьшается с дальнейшим ростом числа нуклонов в ядре. Такая зависимость означает, что для легких ядер энергетически выгоден синтез, а для тяжелых – деление.

График 1. Грубая зависимость удельной  энергии связи ядра от количества нуклонов

Грубый усредненный вид функции зависимости показан на рисунке выше. Современные ядерные модели пытаются объяснить существование и  нескольких малых пиков, связанных с определенным числом нейтронов или протонов в ядре, называемых магическими. В физической литературе утверждается, что ядра, у которых магическое число протонов или нейтронов, устойчивее соседних ядер, а наиболее устойчивы дважды магические ядра, у которых магическое число и протонов и нейтронов. Магические числа для нейтронов: 2, 8, 20, 28, 50, 82, 126, 184. Магические числа для протонов: 2, 8, 20, 28, 50, 82, 114.  Наличие магических чисел имеет следующее объяснение – ядра, так же как и электронные оболочки атомов, имеют оболочную структуру, а магическое число соответствует полностью заполненному слою (оболочке). Однако, любая модель, использующая только представления о магических числах, не будет отражать всех особенностей внутреннего строения ядер атомов. Действительность гораздо сложнее. Попробуем показать это с помощью табличного набора экспериментальных данных. При анализе будем использовать не двумерный график зависимости удельной энергии связи от количества нуклонов, а трехмерную энергетическую поверхность, где двумя измерениями являются количество протонов и количество нейтронов. Такой тонкий анализ показывает, что пики в энергии связи  у магических ядер являются лишь частным случаем. В дальнейшем, символом «p» будем обозначать количество протонов в ядре, а символом «n» - количество нейтронов в ядре. При разрезе энергетической поверхности плоскостью n=p получим график зависимости удельной энергии связи от количества протонов, на котором четко идентифицируется особый пик при n=p=2.

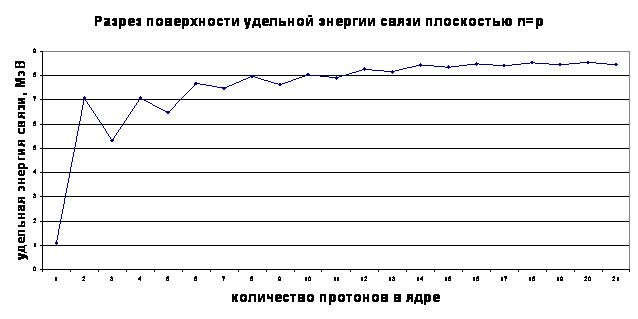
График 2. Разрез поверхности удельной энергии связи ядер плоскостью n=p

В общем случае, пики энергии  связи принадлежат ядрам с четным количеством и протонов и нейтронов, причем  пики стабильных четно-четных ядер простираются несколькими параллельными линиями. Показать это можно не только графически, но с помощью трехмерной таблицы, в которой первое измерение  – количество протонов в ядре, второе измерение – количество нейтронов в ядре, а третьим измерением является удельная энергия связи ядра (МэВ/нуклон).  В таблице изотопов узкую полоску стабильных изотопов называют долиной стабильности. Это неудачное название. Если уж удельную энергию ядра сопоставлять с высотой земной поверхности над уровнем моря, то правильней было бы называть эту полоску не долиной, а  хребтом стабильности. Вдоль этого хребта равномерно расположены линии пиков удельной энергии связи, начинающиеся с линии  p=n.

Таблица 1. Трехмерная таблица изотопов от H до Si

При р=8 в хребте стабильности возникает перелом. Он приобретает зигзагообразный (ступенчатый) вид. При нечетном числе протонов количество стабильных изотопов уменьшается до одного, а при четном числе протонов – увеличивается до трех. Но самое главное – появляется еще одна линия стабильных пиков удельной энергии связи с n=p+2, параллельная начальной линии. Эта линия зарождается при р=4, и становится стабильной при p>=8.  Кроме перелома, второму магическому числу р=8 соответствует повышенное количество долгоживущих изотопов со средним временем жизни t>10сек. Появляется возможность образования пиков стабильности при разном количестве нейтронов и одинаковом количестве протонов. Кроме того, начиная с этого места зарождается новая линия пиков удельной энергии связи с n=p+4. Относительная же амплитуда пика p=8 ничем не выделяется от соседних пиков p=6 и p=4. Это отлично видно, если растянуть график зависимости энергии связи от количества протонов. А магическое число n=8, вопреки утверждениям,  вообще ничем не выделяется.

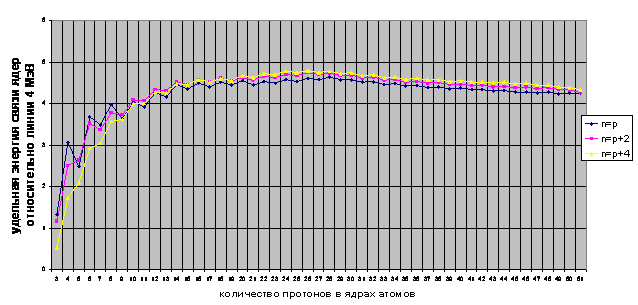
График 3. Растянутые разрезы поверхности удельной энергии связи ядер

При p=10 пики второго хребта становятся выше пиков первого хребта, первых хребет из основного превращается в побочный. При совмещении нескольких разрезов поверхности удельной энергии связи становятся наглядными переходы максимальной амплитуды от одних хребтов к другим. Анализ еще более растянутых графиков позволяет идентифицировать еще три особых пика – p=14, р=20, p=28, из которых лишь числа 20 и 28 являются магическими.

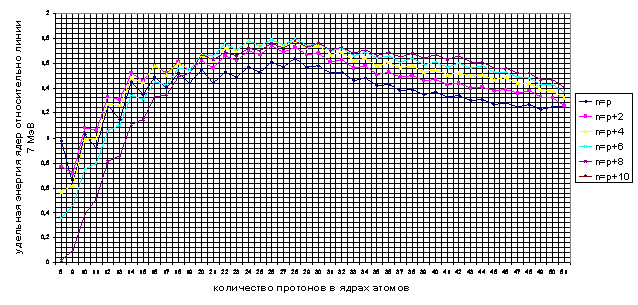
График 4. Совмещение шести разрезов энергетической поверхности

При р=16 в трехмерной таблице изотопов начинается очередная перестройка. Третья линия пиков удельной энергии связи с n=p+4 тоже становится стабильной.

Таблица 2 Трехмерная таблица изотопов от Si до Ni

При р=20 новые изменения - заканчивается первая линия пиков удельной энергии связи и становится стабильной четвертая линия с n=p+6. Кроме того, пики четвертого хребта становятся выше пиков второго хребта, который из основного превращается в побочный.

При р=28 опять изменения - заканчивается вторая линия пиков n=p+2 и становится стабильной пятая линия пиков удельной энергии связи с n=p+8.

Таблица 3. Трехмерная таблица изотопов от Cr  до Se

При n=20, n=28 и n=30  наблюдается повышенное количество стабильных изотопов, из которых лишь числа 20 и 28 являются магическими.

При р=30 новые изменения - заканчивается третья линия пиков n=p+4 и становится стабильной шестая линия пиков удельной энергии связи с n=p+10.

При р=32 снова изменения - становится стабильной седьмая линия пиков удельной энергии связи с n=p+12, а самыми высокими становятся пики шестого хребта n=p+10.

При р=34 становится стабильной восьмая линия пиков удельной энергии связи с n=p+14.

При р=36 заканчивается четвертая линия стабильных пиков n=p+6, а самыми высокими становятся пики седьмого хребта n=p+12.

При р=40 становится стабильной девятая линия пиков удельной энергии связи с n=p+16.

При р=44 заканчивается пятая линия стабильных пиков n=p+8.

При n=40, n=42, n=48, n=50 и n=52   наблюдается повышенное количество стабильных изотопов, из которых лишь число 50 является магическим.

Таблица 4. Трехмерная таблица изотопов от  Ge до Rh

При р=46 становится стабильной десятая линия пиков удельной энергии связи с n=p+18.

Таблица 5. Трехмерная таблица изотопов от  Pd до Te

При р=48 заканчивается шестая линия стабильных пиков n=p+10 и становится стабильной одиннадцатая линия пиков удельной энергии связи с n=p+20.

При р=50 заканчивается седьмая линия стабильных пиков n=p+12 и становится стабильной двенадцатая линия пиков  с n=p+22 и тринадцатая линия пиков с n=p+24.

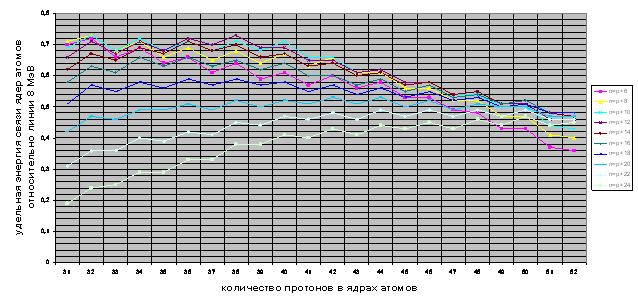
График 5. Совмещение десяти разрезов энергетической поверхности

Анализ особо растянутых графиков позволяет идентифицировать еще один особый пик при p=38,  хотя число 38 и не является магическим. Он формируется линией пиков n=p+12. В свою очередь, при магическом числе p=50 особого пика обнаружить не удается.

p\n	p	p+2	p+4	p+6	p+8	p+10	p+12	p+14	p+16	p+18	p+20	p+22	p+24
1	1,11	1,4	0,96	0,00
2	7,07	4,88	3,93	0,00
3	5,33	5,16	4,53	0,00
4	7,06	6,5	5,72	4,99
5	6,48	6,63	6,1	5,51
6	7,68	7,52	6,92	6,43
7	7,48	7,37	7,04	6,71
8	7,98	7,77	7,57	7,36	7,02	6,5
9	7,63	7,72	7,62	7,46	7,1	6,6
10	8,03	8,08	7,99	7,75	7,39	7
11	7,92	8,06	8	7,80	7,51	7,2
12	8,26	8,33	8,27	8,06	7,81	7,5
13	8,15	8,31	8,26	8,10	7,86	7,6
14	8,45	8,52	8,48	8,34	8,11	7,9	7,66	7,37
15	8,35	8,46	8,45	8,31	8,15	8	7,77	7,53
16	8,49	8,58	8,58	8,45	8,33	8,2	7,99	7,78
17	8,4	8,52	8,51	8,43	8,35	8,2	8,1	7,89
18	8,52	8,61	8,6	8,56	8,49	8,4	8,27	8,08	7,87
19	8,44	8,54	8,55	8,55	8,52	8,4	8,28	8,01	7,9
20	8,55	8,62	8,67	8,67	8,67	8,6	8,4	8,22	8,03
21	8,44	8,56	8,62	8,66	8,63	8,5	8,4	8,23	8,05	7,86
22	8,53	8,66	8,72	8,76	8,69	8,6	8,5	8,31	8,15	7,98
23	8,49	8,62	8,7	8,71	8,66	8,6	8,45	8,31	8,18	8,03
24	8,57	8,7	8,78	8,78	8,72	8,6	8,53	8,42	8,3	8,16
25	8,53	8,67	8,74	8,74	8,7	8,6	8,53	8,43	8,32	8,2
26	8,61	8,74	8,79	8,79	8,76	8,7	8,61	8,51	8,41	8,29	8,18
27	8,57	8,69	8,74	8,75	8,72	8,7	8,6	8,52	8,42	8,32	8,22
28	8,64	8,73	8,78	8,80	8,78	8,7	8,68	8,6	8,52	8,43	8,33	8,23
29	8,57	8,67	8,72	8,74	8,73	8,7	8,65	8,59	8,52	8,44	8,35	8,24
30	8,58	8,68	8,74	8,76	8,76	8,7	8,69	8,64	8,58	8,5	8,43	8,3
31	8,52	8,61	8,67	8,70	8,71	8,7	8,66	8,62	8,58	8,51	8,42	8,31	8,19
32	8,53	8,63	8,69	8,72	8,73	8,7	8,71	8,67	8,63	8,57	8,47	8,36	8,24
33	8,46	8,56	8,62	8,66	8,68	8,7	8,67	8,65	8,61	8,55	8,46	8,36	8,25
34	8,48	8,58	8,64	8,69	8,71	8,7	8,71	8,69	8,66	8,58	8,49	8,4	8,29
35	8,42	8,51	8,58	8,64	8,66	8,7	8,68	8,67	8,63	8,56	8,49	8,39	8,29
36	8,43	8,53	8,61	8,66	8,69	8,7	8,72	8,71	8,66	8,59	8,51	8,42	8,33
37	8,38	8,49	8,56	8,61	8,65	8,7	8,7	8,68	8,63	8,57	8,49	8,41	8,33
38	8,39	8,5	8,58	8,64	8,68	8,7	8,73	8,7	8,65	8,59	8,52	8,45	8,38
39	8,35	8,46	8,53	8,59	8,64	8,7	8,69	8,66	8,62	8,57	8,5	8,44	8,38
40	8,37	8,47	8,55	8,61	8,67	8,7	8,69	8,67	8,64	8,58	8,52	8,47	8,41
41	8,33	8,43	8,51	8,57	8,63	8,7	8,65	8,63	8,6	8,55	8,51	8,46	8,4
42	8,34	8,44	8,52	8,60	8,66	8,7	8,65	8,64	8,6	8,57	8,53	8,48	8,43
43	8,3	8,4	8,5	8,56	8,61	8,6	8,61	8,6	8,57	8,54	8,51	8,46	8,41
44	8,31	8,41	8,51	8,58	8,61	8,6	8,62	8,61	8,59	8,56	8,53	8,49	8,44
45	8,27	8,38	8,47	8,53	8,56	8,6	8,58	8,57	8,55	8,53	8,5	8,47	8,43
46	8,28	8,39	8,49	8,53	8,56	8,6	8,58	8,58	8,57	8,55	8,52	8,49	8,45
47	8,25	8,36	8,44	8,49	8,52	8,5	8,54	8,54	8,53	8,52	8,49	8,47	8,43
48	8,27	8,38	8,44	8,48	8,52	8,5	8,55	8,55	8,54	8,53	8,51	8,49	8,46
49	8,23	8,33	8,39	8,43	8,47	8,5	8,51	8,51	8,51	8,5	8,5	8,47	8,44
50	8,25	8,32	8,38	8,43	8,47	8,5	8,51	8,52	8,52	8,51	8,5	8,49	8,47
51	8,25	8,26	8,32	8,37	8,41	8,4	8,46	8,48	8,48	8,48	8,47	8,46	8,44
52			8,3	8,36	8,4	8,4	8,46	8,47	8,48	8,48	8,47	8,46	8,45

Таблица 6. Итоговая таблица для построения графиков

Подытожим проведенные исследования экспериментальных данных по удельной энергии связи ядер атомов от водорода до теллура. Для построения графиков использовалась компактная итоговая таблица, в которой линии пиков удельной энергии связи  сведены в вертикальные колонки. Зеленым и синим цветом в таблице выделены пики, принадлежащие стабильным изотопам. Простой подсчет количества таких цветных пиков позволяет определить точки перелома:

p=8 – количество стабильных пиков увеличивается до двух;

p=16 – количество стабильных пиков увеличивается до трех;

p=20 – количество стабильных пиков равно пяти;

p=28 – количество стабильных пиков увеличивается до четырех;

p=34 – количество стабильных пиков увеличивается до пяти;

p=48 – количество стабильных пиков увеличивается до шести;

p=50 – количество стабильных пиков увеличивается до семи.

Из исходных таблиц исследуем переломы по общему количеству стабильных изотопов:

p=8 – количество стабильных изотопов увеличивается до трех;

p=16 – количество стабильных изотопов увеличивается до четырех;

p=20 – количество стабильных изотопов равно семи;

p=22 – количество стабильных изотопов равно пяти;

p=28 – количество стабильных изотопов увеличивается до пяти;

p=34 – количество стабильных изотопов увеличивается до шести;

p=42 – количество стабильных изотопов увеличивается до семи;

p=48 – количество стабильных изотопов увеличивается до восьми;

p=50 – количество стабильных изотопов равно десяти.

Теперь исследуем переломы по линиям пиков:

p=2 – начало первой линии  пиков стабильных изотопов;

p=8 – начало второй линии  пиков стабильных изотопов;

p=16 – начало третьей линии пиков стабильных изотопов;

p=20 – начало четвертой линии пиков стабильных изотопов;

p=28 – начало пятой линии пиков стабильных изотопов;

p=30 – начало шестой линии пиков стабильных изотопов;

p=32 – начало седьмой линии пиков стабильных изотопов;

p=34 – начало восьмой линии пиков стабильных изотопов;

p=40 – начало девятой линии пиков стабильных изотопов;

p=46 – начало десятой линии пиков стабильных изотопов;

p=48 – начало одиннадцатой линии пиков стабильных изотопов;

p=50 – начало двенадцатой линии пиков стабильных изотопов.

Окончания линий стабильных пиков тоже являются переломами:

p=20 – конец первой линии  пиков стабильных изотопов;

p=28 – конец второй линии  пиков стабильных изотопов;

p=30 – конец третьей линии пиков стабильных изотопов;

p=36 – конец четвертой линии пиков стабильных изотопов;

p=44 – конец пятой линии пиков стабильных изотопов;

p=48 – конец шестой линии пиков стабильных изотопов;

p=50 – конец седьмой линии пиков стабильных изотопов.

По графикам определили особые пики, выделяющиеся среди соседних пиков по абсолютной или относительной амплитуде :

p=2 – первый особый  пик ;

p=4 – второй особый  пик ;

p=6 – третий особый  пик ;

p=8 – четвертый особый  пик ;

p=14 – пятый особый  пик ;

p=20 – шестой особый  пик ;

p=28 – седьмой особый  пик ;

p=38 – восьмой особый  пик ;

Сведем все сведения об особых точках в одну таблицу, в которой следующие обозначения:

H – количество стабильных пиков;

S – количество стабильных изотопов;

L – начало новой линии стабильных пиков;

K – конец линии стабильных пиков;

A – особые пики, выделяющиеся амплитудой;

Таблица 7. Итоговая таблица для определения магичных чисел для протонов

Аналогично, составим таблицу для определения магичных чисел для нейтронов

Таблица 8. Итоговая таблица для определения магичных чисел для нейтронов

Анализ сводных таблиц позволяет сделать вывод, что официальный список магичных чисел не соответствует экспериментальным данным ни по какому-либо отдельному из исследуемых особых признаков, ни по количеству особых признаков.  Если список магичных чисел составлялся по точкам максимального отклонения теоретических значений удельной энергии связи от экспериментальных значений, то можно с большой вероятностью утверждать, что теоретическая формула для описания энергии связи, если мягко сказать, является несовершенной.

Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru , март 2009 года