Спин и четность ядра
Механистическая модель строения ядер атомов позволяет вернуть спину первоначальный механический смысл. Спин ядра представляет собой сумму спинов составляющих ядро нуклонов с учетом знака спина. Спин нуклона – механический момент вращения. Его величина зависит от скорости вращения нуклона вокруг собственной оси и от расстояния до оси измерения, чаще всего являющейся и осью симметрии ядра. Так как собственное вращение нуклона постоянно, то изменяться может только расстояние до оси измерения.
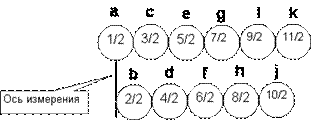

Рисунок 1. Спин нуклона в зависимости от расстояния до оси
При плотной упаковке расстояние до оси измерения принимает только дискретные величины, кратные радиусу нуклона. Соответственно, спин нуклона тоже может иметь только дискретные значения, так как, согласно данной модели, все вектора моментов вращения параллельны оси измерения. Для точного подсчета спина ядра достаточно знать точное расстояние от каждого нуклона до оси симметрии и ориентацию спина нуклона. Это возможно при наличии графического изображения пространственной конфигурации ядра. Но с графическим изображением не всегда удобно работать. Иногда необходимо использовать математическое либо символьное описание. Существующее символьное описание электронных оболочек для данного случая явно не подходит - нет четкой системы обозначений. Обозначение должно естественным образом указывать на относительную координату нуклона в ядре.
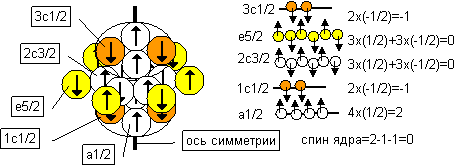
Рисунок 2. Пример вычисления спина ядра
При плотной упаковке нуклоны располагаются слоями. Для удобства символьного описания, присвоим каждому слою уникальное обозначение, используя буквы латинского алфавита последовательно. Начальную букву алфавита используем для обозначения нуклонов, находящихся на оси симметрии. Последующие буквы алфавита будем последовательно использовать для обозначения нуклонов, находящихся на последующих дискретных расстояниях (орбитах) от оси симметрии (измерения). Нуклоны, находящиеся на орбите ‘c’, кроме вращения вокруг собственной оси могут еще вращаться по орбите вокруг оси симметрии (2-3 нуклона с одинаковым направлением спина). В этом случае суммарный спин нуклона уменьшается до значения “1/2”. Во всех остальных случаях нуклоны не имеют орбитального вращения и имеют суммарный спин согласно рисунку выше.
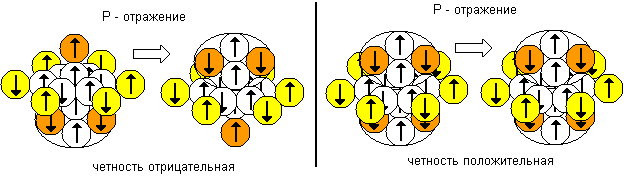
Рисунок 3. Пример вычисления четности ядра
Четность ядра тоже вычисляется легко. При инверсии координат каждого нуклона (x на –x, y на –y, z на –z, то есть при P-отражении) конфигурация ядра с отрицательной четностью изменяется, а конфигурация ядра с положительной четностью не изменяется. Направление спина нуклона при P-отражении не меняется. На рисунке ниже приведены примеры вычисления четности. Во втором случае отраженные ядра полностью идентичны, поэтому четность положительная. В первом случае отраженные ядра внешне похожи, если одно из ядер развернуть на 180 градусов. Но физическими свойствами они все же будут отличаться, так как не совпадает направление спинов у шести нуклонов. Поэтому у этих ядер четность отрицательная. Отраженные ядра имеют одинаковый по абсолютной величине спин, но направление спина противоположное при одинаковой ориентации ядер в пространстве.
Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru , январь 2008 года