Проявление торсионокинетической силы смещения
В газовой среде по разным причинам возможно формирование областей c разным давлением. Следствием этого становится движение газа из области повышенного давления в область пониженного. Назовем ламинарное течение любого газа ветром – общепринятым термином для обозначения подобных явлений в атмосфере Земли. При своем движении газ увлекает в движение и находящиеся в нем объекты. Рассмотрим несколько частных случаев движения свободных твердотельных объектов, не имеющих вращения. Для упрощения условий допустим, что все объекты сферические и появляются мгновенно в области ламинарного течения газа (ветра).

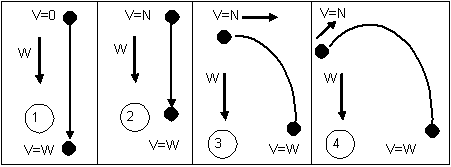
Рисунок 1. Воздействие ветра на не вращающиеся сферические объекты
В первом случае мгновенно появляется покоящийся объект. Под действием ветра объект придет в движение. Траекторией станет прямая, параллельная вектору скорости ветра. В начале траектории скорость объекта V=0. Из-за наличия инерции потребуется некоторое время, по истечении которого скорость объекта достигнет скорости ветра V=W. Во втором случае объект уже имеет начальную скорость N, вектор которой параллелен вектору скорости ветра. Траекторией опять будет прямая, а по истечении времени переходных процессов скорость движения объекта будет опять равна скорости ветра, только времени для достижения этой скорости потребуется меньше. В третьем случае вектор начальной скорости перпендикулярен вектору скорости ветра. В этом случае траекторией будет ниспадающая дуга. После истечения времени переходных процессов дуга перерастет в прямую линию, на которой вектор скорости объекта будет равен вектору скорости ветра. Первоначальная поперечная составляющая скорости исчезнет из-за наличия сопротивления движению со стороны воздуха. В четвертом случае между вектором начальной скорости объекта и вектором ветра тупой угол. Траектория объекта на этот раз будет самой сложной. После окончания переходных процессов снова вектор скорости объекта будет равен вектору скорости ветра. Но в течение времени переходных процессов траектория будет состоять из двух дуг. Двигаясь по одной дуге, объект будет терять до нуля первоначальную продольную составляющую скорости. Двигаясь по другой дуге, объект будет увеличивать продольную составляющую скорости от нуля до скорости ветра.
Поведение вращающихся объектов при наличии ветра отличается коренным образом от поведения невращающихся тел. Убойная дальность нарезного оружия выше, чем гладкоствольного. Это означает, что воздух оказывает значительно меньшее лобовое сопротивление вращающейся пуле. Причина этого хорошо изучена и кроется в гироскопическом эффекте, благодаря которому пуля не кувыркается. Удивительно то, что вращающаяся пуля мало подвержена воздействию бокового ветра. Она практически не смещается от первоначального направления, а лишь начинает двигаться по спиральной траектории. Поэтому и точность ее попадания в цель значительно выше.
Полет бумерангов австралийских аборигенов до сих пор удивляет своей оригинальностью. Но и в этом нет никакого колдовства. Карьер экспериментально зафиксировал поведение в воздухе легких однородных сферических ядер, вращающихся вокруг оси, перпендикулярной плоскости траектории центра. Результаты даны в статье в Journal de Physique theorique et appliquée, т.V, 1916. При постоянном вращении получаются траектории, которые имеют асимптоты, наклоненные в ту или иную сторону, в зависимости от направления вращения. Эксперименты с ядрами провести дано не каждому. Но любой человек может поэкспериментировать с пластиковыми дисками. Поведение брошенного вращающегося диска аналогично поведению ядер Карьера.
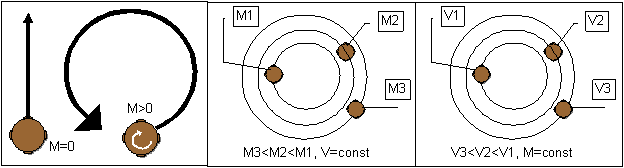
Рисунок 2. Траектории брошенных дисков (вид с верху)
Если запустить невращающийся диск (момент вращения М=0) параллельно поверхности Земли, то его поведение обычно – проекция траектории на горизонтальную плоскость прямолинейна. Если вращающийся диск (M>0) отпустить без горизонтальной составляющей скорости, то он просто упадет на Землю под действием гравитации аналогично любому другому предмету – траекторией будет вертикальная прямая. Но если диск бросить и при броске закрутить (ось вращения должна быть перпендикулярна вектору скорости), то он опишет в воздухе окружность и вернется к исходному месту. Чем больше момент вращения при одной и той же скорости, тем меньше диаметр описываемой окружности. Чем меньше начальная скорость диска, тем больше диаметр описываемой окружности.
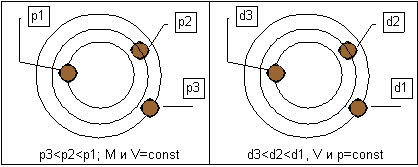
Рисунок 3. Траектории при разной плотности среды и разных диаметрах дисков
Более тщательный эксперимент показывает, что существуют потери - из-за трения о воздух падает и момент вращения диска, и скорость его движения. По этим причинам формой горизонтальной проекции траектории брошенного вращающегося диска является не окружность, а расходящаяся плоская спираль с постоянно увеличивающимся радиусом.
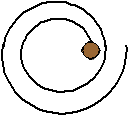
Рисунок 4. Реальная траектория вращающегося диска (вид с верху)
Странной круговой траектории находится простое физическое объяснение. Движение диска относительно неподвижного воздуха равносильно движению воздуха относительно неподвижного диска, то есть равносильно появлению ветра. Лобовое сопротивление воздуха становится для диска как бы твердой опорой, по которой он начинает катиться в бок. Но при этом поворачивается вектор результирующей скорости, что равносильно постепенному повороту твердой опоры (постепенной смене направления ветра). Конечным результатом идеального взаимодействия диска с воздухом (при отсутствии потерь) является круговая траектория. Но потери энергии диска все же неизбежны. Большая часть энергии вращения уходит на увлечение во вращение окружающего воздуха.

Рисунок 5. Спиральные вихри на диске, вращающемся со скоростью 1800 об/мин.
(Ван-Дайк М. - Альбом течений жидкости и газа, фото 132)
Анализируя поведение вращающегося ядра или диска можно сделать вывод, что для математического описания его движения нужно ввести дополнительную силу, вектор которой всегда перпендикулярен вектору ветра и вектору момента вращения. То есть, на движущийся относительно неподвижного воздуха диск, момент вращения которого перпендикулярен скорости, всегда действует сила смещения, перпендикулярная и моменту вращения и скорости. Направление силы определяется по правилу правого буравчика при повороте от вектора скорости к вектору момента вращения. Амплитуда силы пропорциональна произведению амплитуд векторов скорости и момента вращения. Сила смещения растет с ростом амплитуды любого из векторов и исчезает при исчезновении любого из векторов. С математической точки зрения это есть векторное произведение векторов и в символьном виде записывается следующим образом: F=k[VxM], где
F – вектор силы смещения, действующей дополнительно на диск;
k – коэффициент пропорциональности;
V – вектор скорости диска относительно газовой среды;
x – математическое обозначение операции векторного умножения;
M – вектор момента вращения диска.
Так как данная сила смещения возникает только при наличии вращения и движения относительно среды, то для отличия от каких-либо других сил нужно дать ей специальное название. Назовем ее торсионно-кинетической силой смещения.

Рисунок 6. Относительное положение вектора смещения
В рассмотренных выше случаях ось вращения была всегда перпендикулярна плоскости траектории. Для дисков другого варианта быть не может – они начнут планировать. А вот с ядрами производились такие эксперименты, в которых мгновенная ось вращения имела произвольное, но известное направление. В этом случае траектория была пространственной кривой. Формулу F=k[VxM] можно использовать и для таких ситуаций, только V – в данном случае не полная скорость, а составляющая полной скорости, перпендикулярная вектору момента вращения.
Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru , май 2006 года