НА ГЛАВНУЮ СТРАНИЦУ

Вращающееся тело на круговой орбите

Принято считать, что в макромире дискретные уровни энергий обычно присущи только механическим колебательным системам (струна, пластина, колокол и т.п.). Попробуем развеять эти заблуждения. Ранее было рассмотрено поведение вращающегося тела при наличии ветра, направление которого перпендикулярно оси вращения. При таких начальных условиях возможно несколько типов траектории движения оси вращения.  Если V - собственная мгновенная скорость тела, а W – скорость ветра, то  при V/W<1 возникает торсионно-кинетическая сила, смещающая тело в сторону, перпендикулярную направлению ветра.  Траектория тела в этом случае будет иметь вид гиперболы при быстром затухании вращения и периодической с периодом в виде полукольца, если вращение не затухает.

Рисунок 1.  Траектория тела при незатухающем вращении при V/W<1

 При V/W>1 в траектории движения появляются  участки с движением навстречу ветру. Если скорости V и W соизмеримы, то траектория имеет петлистый вид. При возрастании отношения V/W траектория становится спиральной. Если V/W стремится к бесконечности, то форма траектории стремится к окружности. Форма траектории не зависит от системы координат. Выберем систему координат, которая движется равномерно и прямолинейно вместе с ветром. В такой системе скорость ветра равна нулю, а ось вращения тела под действием сил инерции движется в одной плоскости по петлевой спиральной траектории в определенном  линейном направлении.

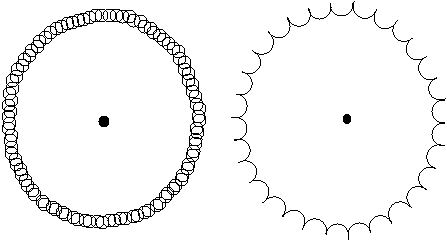
Рисунок 2.  Два типа траектории вращающегося тела на круговой орбите

Теперь представим, что на вращающееся тело, движущееся под действием сил инерции, в плоскости, перпендикулярной оси вращения тела, дополнительно воздействует центрально-симметричное поле неких сил притяжения. В этом случае средняя линейная траектория  должна замкнуться. А форма траектории тела может иметь либо вид замкнутой петлевой спирали, либо звездообразный вид. В любом случае мы имеем дело с волновым движением. В общем случае, если центральное поле действительно имеет абсолютную круговую симметрию, то не имеет значения соотношение длины орбиты к длине волны. Орбитальное движение всегда будет устойчивым после окончания переходных процессов. Но если источник поля в центре либо пульсирует, либо сам вращается вокруг собственной оси, совершая биения, то ситуация меняется кардинальным образом. В этом случае симметричность нарушается. У центрального поля появляются максимумы и минимумы воздействия. Тогда устойчивой будет только такая орбита, у которой впадины и выпуклости волновой траектории совпадают с максимумами и минимумами воздействия при каждом обороте вокруг источника центрального поля. Такое станет возможным, если на орбите уложится целое число волн. Как видно на рисунке ниже, минимальное количество – три волны.

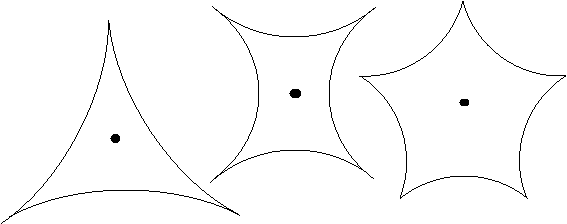
Рисунок 3.  Траектории с тремя, четырьмя и пятью волнами

С другой стороны, нет никаких ограничений на максимальное количество волн. Назовем устоявшиеся орбиты с целым числом волн стационарными. Каждой стационарной орбите мы можем присвоить номер, равный количеству волн. Тогда для каждой орбиты мы можем определить две соседние орбиты, у которых количество волн либо больше на единицу, либо меньше на единицу.  Например, у четвертой орбиты соседними являются третья и пятая орбита. На каждой орбите движущееся тело имеет собственную полную энергию, отличную от энергии на любой из других орбит. Легко заметить, что траектории тела на соседних орбитах с малыми номерами резко отличаются друг от друга. С другой стороны, траектории тела на соседних орбитах с большими номерами практически невозможно отличить. Например, траектории на орбитах с номерами 9998 и 9999 на любом рисунке будут одинаково выглядеть. Вполне логичен вывод, что чем больше номер, тем меньше отличаются друг от друга полные энергии тела на соседних орбитах (меньше разность полных энергий). Мы имеем дело с макроскопической системой с дискретным набором энергий. Какие же физические процессы могут происходить в источнике центрального поля, способного создавать максимумы и минимумы силы притяжения в плоскости орбитального вращения его спутника, вращающегося вокруг собственной оси?

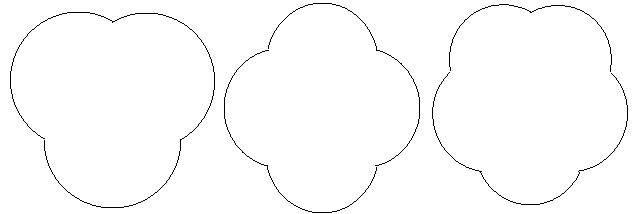
Рисунок 4.  Объемные колебания жидкой капли с 3, 4 и 5 пучностями

Нагляднее всего рассмотреть самый простой физический процесс – объемные колебания жидкой капли. Такие колебания так же, как и при колебаниях струны, должны иметь узлы и пучности. В пучностях амплитуды колебаний максимальны, а в узлах минимальны. Так же, как и при колебаниях струны, чем меньше количество пучностей, тем больше их амплитуда и энергия колебаний, тем большая энергия нужна для возбуждения такой моды. Могут быть и другие физические объекты, способные создавать максимумы и минимумы воздействия центрального силового поля. Далеко ходить не будем, и продолжим мысленные эксперименты с жидкой каплей. В первом случае мы рассмотрели объемные колебания капли с нулевым моментом вращения.

Теперь создадим более сложный гипотетический объект. Пусть жидкая капля вращается вокруг собственной оси. Допустим, что существует некий физический процесс, способствующий делению вращающейся капли. С точки зрения гидродинамики вращающаяся капля является вихрем. При взаимодействии четного количества подобных вихрей может образоваться комбинация слипшихся вихрей, если любые соседние вихри имеют противоположное направление вращения. В таких объектах максимум воздействия находится в точках, максимально приближенных к орбите спутника.

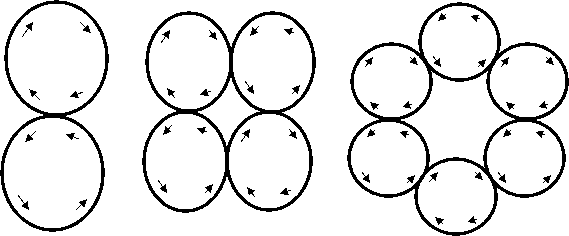
Рисунок 5.  Вихревые комбинации с 2, 4 и 6 максимумами воздействия

Раз уж речь зашла о вихрях, то нельзя пройти мимо тороидального вихря. Однако физические процессы в нем при объемных колебаниях подобны колебаниям жидкой капли, поэтому  ничего нового рисунки его объемных колебаний не дадут.

Продолжим мысленные эксперименты с жидкой каплей. Теперь представим, что в капле симметрично по экватору возникают домены одинаковой величины и равноудаленные друг от друга. Внутри доменов бушуют некие одинаковые физические процессы, сопровождающиеся выбросами вещества или излучения, похожие на фонтаны или гейзеры. Тогда эти фонтаны будут отталкивать спутник на орбите, поэтому в данных точках будут минимумы сил притяжения, а между фонтанами будут действовать максимумы сил притяжения.

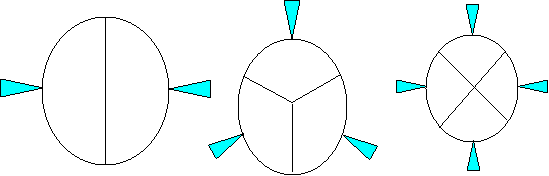
Рисунок 6.  Объекты с двумя, тремя и четырьмя симметричными выбросами

Таким образом, рассмотрено несколько принципов образования макроскопических систем, в которых действуют реальные законы макромира, но образуются орбиты с дискретными уровнями энергий.

Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru , декабрь 2012 года