
Воздействие ветра на вращающиеся тела
При движении вращающегося диска относительно неподвижного воздуха, как было показано ранее, возникает торсионокинетическая сила смещения. Под действием этой силы траекторией диска становится расходящаяся плоская спираль с постоянно увеличивающимся радиусом. Теперь попробуем использовать настоящий ветер. А диск будем отпускать с вышки таким образом, чтобы он просто падал плоскостью вниз под действием гравитации. Теперь сверху проследим траектории диска в зависимости от скорости вращения. Мы сможем наблюдать только горизонтальную составляющую скорости, а именно это нас и интересует.

Рисунок 1. Рост торсионокинетической силы смещения
При нулевом моменте вращения (M=0) никаких сил смещения не возникает. Диск либо спланирует непредсказуемым образом, либо как обычно будет сдуваться ветром, а его траектория сверху будет выглядеть в виде прямой линии, параллельной направлению ветра. Это нормальная классическая траектория. Если же отпускать вращающийся диск, то он уже полетит по дуге. Траектория прямой линией уже не будет, так как появляется сила смещения. Постепенно увеличивая скорость вращения сбрасываемых дисков, можно будет наблюдать качественное изменение вида траектории при постоянной скорости ветра. При малых скоростях вращения диск начнет сначала двигаться по дуге, отклоняясь от траектории с M=0, а затем перейдет на прямую, параллельную этой траектории. Скорость диска на прямой траектории всегда равна скорости ветра, поэтому относительно воздуха он не будет иметь скорости и смещаться не сможет. Чем больше скорость вращения диска, тем дальше он отклонится от нормальной траектории. При некотором моменте вращения М3 собственная мгновенная скорость диска V, относительно неподвижной системы координат, на дугообразном участке траектории достигнет скорости ветра W. При этом диск опишет четверть окружности, и его траектория перейдет в прямую.
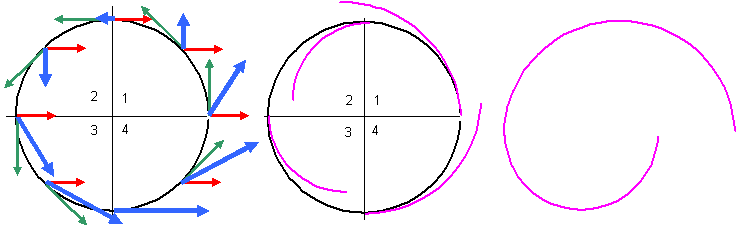
Рисунок 2. Искажение круговой траектории от воздействия ветра
При дальнейшем увеличении скорости вращения диска должен произойти качественный скачок – переход на круговую траекторию. Но воздействие ветра искажает круговую траекторию. Можно оценить вид искажений. Для этого определим в нескольких точках круговой траектории действительную скорость диска относительно окружающей газовой среды. Геометрически - это разница векторов собственной скорости диска по круговой траектории и скорости ветра, что равносильно геометрической сумме вектора собственной скорости и вектора, противоположного скорости ветра. В результате получим, что в первой и четвертой четвертях окружности действительная скорость уменьшается, а во второй и третьей четвертях – увеличивается. Из ранее введенной формулы F=k[VxM] следует, что в первой и четвертой четвертях радиус траектории увеличивается, а во второй и третьей четвертях радиус траектории уменьшается. В результате круговая траектория искажается до петли. Таким образом, воздействие ветра приводит к петлевой спиральной траектории вращающегося диска.
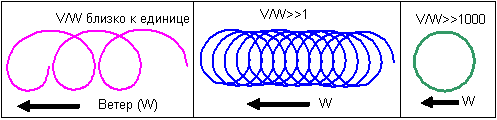
Рисунок 3. Траектории дисков при постоянном ветре, но разном отношении V/W
Переход на круговую траекторию происходит при V/W>1 (V - собственная скорость диска, W – скорость ветра). Максимальные искажения круговой траектории должны происходить при малых значениях этого отношения. При больших значениях (V/W>>1) искажения незначительны, в этих случаях траектория диска будет мало отличаться от круговой траектории. Именно такое физическое явление и происходит при полете очень быстро вращающейся пули.
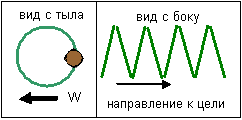
Рисунок 4. Траектория сверх быстро вращающейся пули при ветре
Под действием бокового ветра гипотетическая пуля со сверхбыстрой скоростью вращения будет лишь двигаться по окружности малого радиуса, но не сместится от направления к цели. А в совокупности с движением к цели полная траектория станет винтовой. При полете реальной пули возникает незначительный боковой снос, так как боковая составляющая траектории представляет собой петлевую спираль. Чем меньше скорость вращения, тем будет больше снос при одной и той же силе ветра. В направлении к цели летящая пуля движется относительно среды, но момент вращения параллелен этой составляющей скорости и силы смещения не возникает. Сила смещения возникает лишь при наличии составляющей скорости, перпендикулярной вектору момента вращения. В данном случае такая составляющая скорости возникает при любом боковом ветре. Под действием бокового ветра линейная траектория пули превращается в винтовую траекторию.

Рисунок 5. Траектория сверх быстро вращающегося диска
Движение среды относительно пули равносильно движению пули относительно неподвижной среды. Если боковой ветер не в состоянии отклонить пулю со сверхбыстрой скоростью вращения, значит можно сделать вывод, что такая пуля не оказывает боковому ветру практически никакого сопротивления. Если такой пуле каким-либо образом придать боковую скорость, то она могла бы длительное время двигаться в этом направлении по петлевой спиральной траектории, не теряя скорости движения. Проблема только в том, что пуля может повернуться острием к ветру. Объект должен иметь форму диска, тогда он не повернется. Движение в выделенном направлении в этом случае должно осуществляться по инерции. Вращение диска будет являться с одной стороны причиной колебаний при движении, а с другой стороны – причиной длительного движения без сопротивления среды. Плотность среды не имеет значения, даже жидкая среда не будет оказывать сопротивления. Но до перехода к такому способу движения диск должен набрать скорость в выделенном направлении с помощью какого-либо двигателя (турбовинтового, реактивного и пр.). Впрочем, наверное, возможно постоянно увеличивать или уменьшать скорость с помощью специализированных двигателей непосредственно в режиме движения без сопротивления среды.
Возможен оригинальный способ передвижения с использованием момента вращения диска. Если техническое устройство в форме диска (тарелки) способно менять направление момента вращения, не изменяя при этом скорости вращения, то оно способно и к целенаправленному движению в газообразной или жидкой среде переменными галсами. Только, в отличие от траектории парусника, двигающегося таким способом против ветра, траектория диска будет не ломаной, а криволинейной. Скорость вращения диска в этом случае должна быть намного меньше, чем при движении без сопротивления среды.
![]()
Рисунок 6. Способ целенаправленного движения вращающегося диска
Наличие ветра равносильно наличию движения относительно среды. Из формулы F=k[VxM] следует, что неподвижное относительно среды вращающееся тело не может приобрести направленное движение. Для того чтобы начать движение из одного пункта в другой, необходимо либо дождаться ветра, либо задать диску с помощью какого-либо двигателя (например, турбовинтового или реактивного) начальную скорость в боковом направлении от направления на пункт назначения. Под действием торсионокинетической силы смещения диск начнет двигаться по окружности и в моменты, когда он начнет пересекать прямую линию между двумя пунктами, нужно менять направление момента вращения. Для того чтобы реже менять направление момента вращения, нужно чтобы радиус круговой траектории был как можно больше. А больший радиус траектории при постоянной скорости диска достигается при большем диаметре диска, при меньшей плотности газовой среды, при меньшей скорости вращения диска.
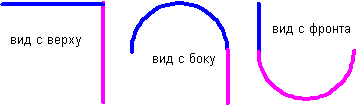
Рисунок 7. Траектория диска при повороте момента вращения на 90 градусов
При повороте направления момента вращения на 180 градусов одна круговая траектория должна плавно переходить в другую круговую траекторию в одной и той же плоскости. При повороте на 90 градусов траектория преломится и перейдет в перпендикулярную плоскость, что немыслимо для классических летающих технических средств. При повороте момента вращения на угол меньше 90 градусов направленного движения к пункту Б осуществить невозможно, так как диск начнет возвращаться в исходный пункт.

Рисунок 8. Целенаправленное движение диска со сменой способов движения
В течение времени перемещения из одного пункта в другой способы движения могут многократно меняться.
Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru , май 2006 года